Lissajous Curve Table by FellippeHeitor

[Qwerkey]

Lissajous Curve Table

Author: @FellippeHeitor
Source: qb64.org Forum
URL: https://www.qb64.org/forum/index.php?topic=683.0
Version: « Reply #8 on: October 09, 2018, 02:48:07 PM »
Tags: [2D], [Graphics], [Mathematics]

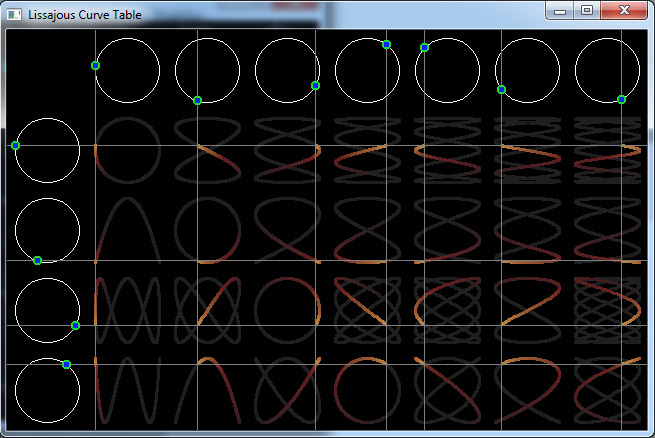
Description:
Graphical Lissajou's Figures.  For added eye-candy-ness, I've changed the plot line to paint using HSB colors so that ink color will vary according to the current rotational angle.

Source Code:

Code: QB64: [Select]

1. _TITLE "Lissajous Curve Table"
2.  
3. $RESIZE:ON
4.  
5. TYPE vector
6.     x AS SINGLE
7.     y AS SINGLE
8. END TYPE
9.  
10. DIM SHARED angle
11. DIM SHARED w
12. DIM SHARED rows, cols
13.  
14. SCREEN _NEWIMAGE(800, 800, 32)
15.  
16. setup:
17. angle = 0
18. w = 80
19. rows = INT(_HEIGHT / w) - 1
20. cols = INT(_WIDTH / w) - 1
21. REDIM dot(rows, cols) AS vector
22.  
23. plot = _NEWIMAGE(_WIDTH, _HEIGHT, 32)
24. _DEST plot
25. CLS
26. _DEST 0
27.  
28. DO
29.     IF _RESIZE THEN
30.         oldScreen = _DEST
31.         SCREEN _NEWIMAGE(_RESIZEWIDTH, _RESIZEHEIGHT, 32)
32.         _FREEIMAGE oldScreen
33.         _FREEIMAGE plot
34.         GOTO setup
35.     END IF
36.  
37.     _PUTIMAGE , plot
38.  
39.     d = w - 0.2 * w
40.     r = d / 2
41.  
42.     FOR i = 0 TO cols
43.         cx = w + i * w + w / 2
44.         cy = w / 2
45.         CIRCLE (cx, cy), r
46.  
47.         x = r * COS(angle * (i + 1) - _PI(.5))
48.         y = r * SIN(angle * (i + 1) - _PI(.5))
49.  
50.         LINE (cx + x, 0)-(cx + x, _HEIGHT), _RGB32(127, 127, 127)
51.         CircleFill cx + x, cy + y, 4, _RGB32(28, 222, 50)
52.         CircleFill cx + x, cy + y, 2, _RGB32(11, 33, 249)
53.  
54.         FOR j = 0 TO rows
55.             dot(j, i).x = cx + x
56.         NEXT
57.     NEXT
58.  
59.     FOR i = 0 TO rows
60.         cx = w / 2
61.         cy = w + i * w + w / 2
62.         CIRCLE (cx, cy), r
63.  
64.         x = r * COS(angle * (i + 1) - _PI(.5))
65.         y = r * SIN(angle * (i + 1) - _PI(.5))
66.  
67.         LINE (0, cy + y)-(_WIDTH, cy + y), _RGB32(127, 127, 127)
68.         CircleFill cx + x, cy + y, 4, _RGB32(28, 222, 50)
69.         CircleFill cx + x, cy + y, 2, _RGB32(11, 33, 249)
70.  
71.         FOR j = 0 TO cols
72.             dot(i, j).y = cy + y
73.         NEXT
74.     NEXT
75.  
76.     _DEST plot
77.     LINE (0, 0)-(_WIDTH, _HEIGHT), _RGBA32(0, 0, 0, 4), BF
78.     FOR j = 0 TO rows
79.         FOR i = 0 TO cols
80.             CircleFill dot(j, i).x, dot(j, i).y, 1, hsb(_R2D(angle), 127, 127, 255)
81.         NEXT
82.     NEXT
83.  
84.     angle = angle + 0.01
85.     IF angle > _PI(2) THEN angle = 0
86.  
87.     _DEST 0
88.  
89.     _DISPLAY
90.     _LIMIT 30
91. LOOP
92.  
93. SUB CircleFill (x AS LONG, y AS LONG, R AS LONG, C AS _UNSIGNED LONG)
94.     DIM x0 AS SINGLE, y0 AS SINGLE
95.     DIM e AS SINGLE
96.  
97.     x0 = R
98.     y0 = 0
99.     e = -R
100.     DO WHILE y0 < x0
101.         IF e <= 0 THEN
102.             y0 = y0 + 1
103.             LINE (x - x0, y + y0)-(x + x0, y + y0), C, BF
104.             LINE (x - x0, y - y0)-(x + x0, y - y0), C, BF
105.             e = e + 2 * y0
106.         ELSE
107.             LINE (x - y0, y - x0)-(x + y0, y - x0), C, BF
108.             LINE (x - y0, y + x0)-(x + y0, y + x0), C, BF
109.             x0 = x0 - 1
110.             e = e - 2 * x0
111.         END IF
112.     LOOP
113.     LINE (x - R, y)-(x + R, y), C, BF
114. END SUB
115.  
116. FUNCTION map! (value!, minRange!, maxRange!, newMinRange!, newMaxRange!)
117.     map! = ((value! - minRange!) / (maxRange! - minRange!)) * (newMaxRange! - newMinRange!) + newMinRange!
118. END FUNCTION
119.  
120. FUNCTION hsb~& (__H AS _FLOAT, __S AS _FLOAT, __B AS _FLOAT, A AS _FLOAT)
121.     DIM H AS _FLOAT, S AS _FLOAT, B AS _FLOAT
122.  
123.     H = map(__H, 0, 255, 0, 360)
124.     S = map(__S, 0, 255, 0, 1)
125.     B = map(__B, 0, 255, 0, 1)
126.  
127.     IF S = 0 THEN
128.         hsb~& = _RGBA32(B * 255, B * 255, B * 255, A)
129.         EXIT FUNCTION
130.     END IF
131.  
132.     DIM fmx AS _FLOAT, fmn AS _FLOAT
133.     DIM fmd AS _FLOAT, iSextant AS INTEGER
134.     DIM imx AS INTEGER, imd AS INTEGER, imn AS INTEGER
135.  
136.     IF B > .5 THEN
137.         fmx = B - (B * S) + S
138.         fmn = B + (B * S) - S
139.     ELSE
140.         fmx = B + (B * S)
141.         fmn = B - (B * S)
142.     END IF
143.  
144.     iSextant = INT(H / 60)
145.  
146.     IF H >= 300 THEN
147.         H = H - 360
148.     END IF
149.  
150.     H = H / 60
151.     H = H - (2 * INT(((iSextant + 1) MOD 6) / 2))
152.  
153.     IF iSextant MOD 2 = 0 THEN
154.         fmd = (H * (fmx - fmn)) + fmn
155.     ELSE
156.         fmd = fmn - (H * (fmx - fmn))
157.     END IF
158.  
159.     imx = _ROUND(fmx * 255)
160.     imd = _ROUND(fmd * 255)
161.     imn = _ROUND(fmn * 255)
162.  
163.     SELECT CASE INT(iSextant)
164.         CASE 1
165.             hsb~& = _RGBA32(imd, imx, imn, A)
166.         CASE 2
167.             hsb~& = _RGBA32(imn, imx, imd, A)
168.         CASE 3
169.             hsb~& = _RGBA32(imn, imd, imx, A)
170.         CASE 4
171.             hsb~& = _RGBA32(imd, imn, imx, A)
172.         CASE 5
173.             hsb~& = _RGBA32(imx, imn, imd, A)
174.         CASE ELSE
175.             hsb~& = _RGBA32(imx, imd, imn, A)
176.     END SELECT
177.  
178. END FUNCTION
179.